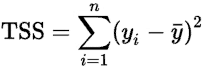Многие компании используют регрессионный анализ для прогнозирования непрерывной зависимой переменной от нескольких независимых переменных. Аналитики данных и финансовые специалисты используют регрессионный анализ для определения силы предикторов, для прогнозирования эффекта или для прогнозирования тенденций. Одним из первых расчетов в регрессионном анализе является сумма квадратов.
В этой статье мы обсудим, что такое сумма квадратов, формулу суммы квадратов, как рассчитать сумму квадратов и различные виды суммы квадратов, а также пример расчета.
Что такое сумма квадратов?
Сумма квадратов (SS) - это инструмент, который используют статистики и ученые для оценки общего отклонения набора данных от среднего значения. Этот статистический инструмент показывает, насколько хорошо данные соответствуют своей модели, особенно в регрессионном анализе.
Как один из наиболее важных результатов регрессионного анализа, SS используется для того, чтобы показать вариацию в данных, так что меньшая сумма квадратов показывает лучшую модель, а большая сумма квадратов - меньшую. Чем меньше или больше сумма, тем меньше или больше отдельные точки данных отклоняются от среднего значения. Если сумма равна нулю, ваша модель идеально подходит.
Например, финансовые консультанты могут использовать SS для расчета разницы в ежедневной стоимости акций. Когда СС является большим числом, это означает, что стоимость акций имеет большое отклонение от среднего значения, что свидетельствует о нестабильности рынка. Когда SS - небольшое число, это означает, что стоимость акций имеет небольшое отклонение от среднего значения, что свидетельствует о стабильности рынка. Квадратный корень из суммы квадратов - это стандартное отклонение, которое также является полезным числом для финансовых консультантов.
Формула суммы квадратов
Формула суммы квадратов - это математический способ нахождения модели, которая меньше всего отличается от данных. Полезно отметить, что специалисты иногда называют сумму квадратов так вариация. Вот формула, используемая для нахождения общей суммы квадратов, наиболее распространенной вариации этого расчета:
В этом уравнении:
-
Yi = i-тый термин в наборе
-
ȳ = среднее значение всех предметов в наборе
Как рассчитать сумму квадратов
Ниже приведены шаги, которые вы можете выполнить для расчета суммы квадратов:
1. Подсчитайте количество измерений
Буква n обозначает размер выборки, который также является количеством измерений.
2. Вычислите среднее значение
Среднее - это среднее арифметическое значение выборки. Для этого нужно сложить все измерения и разделить на объем выборки, n.
3. Вычтите каждое измерение из среднего значения
Если у вас есть числа, превышающие среднее значение, то они дадут отрицательное число, и это нормально. У вас должна быть серия из n индивидуальных отклонений от среднего значения.
4. Возведите в квадрат разницу между каждым измерением и средним значением
Результат возведения числа в квадрат всегда положителен, поэтому если в предыдущем шаге у вас были отрицательные числа, то теперь они будут положительными. У вас должна быть серия из n положительных чисел.
5. Сложите квадраты вместе и разделите на (n-1)
На последнем этапе вы должны получить сумму квадратов. Эта сумма квадратов является стандартной дисперсией для вашего объема выборки.
Пример суммы квадратов
Приведем пример задачи, в которой следуют описанные выше шаги для решения суммы квадратов для чисел 2, 4 и 6:
1. Подсчитать
Подсчет количества измерений. Количество измерений - это объем выборки, обозначается буквой n.
n = 3
2. Рассчитайте
Сложите все измерения и разделите на объем выборки, чтобы найти среднее значение.
(2+4+6)3 = 123 = 4
3. Вычесть
Вычтите каждое измерение из среднего значения.
4 - 2 = 2
4 - 4 = 0
4 - 6 = -2
4. Квадрат
Возведите в квадрат разность каждого измерения от среднего значения, чтобы получить серию из n положительных чисел.
22 = 4
02 = 0
(-2)2 = 4
5. Добавить
Сложите квадраты вместе, чтобы найти сумму квадратов, также известную как стандартная дисперсия для вашего объема выборки.
4 + 0 + 4 = 8
Типы суммы квадратов
Существует три основных типа суммы квадратов: общая сумма квадратов, сумма квадратов регрессии и остаточная сумма квадратов. Вот краткое объяснение каждого типа:
Общая сумма квадратов
Формула общей суммы квадратов, продемонстрированная выше, говорит о том, насколько велика вариация зависимой переменной, и количественно определяет общую вариацию выборки.
Иногда фактические квадраты представляют собой общую сумму квадратов вдоль линии регрессии графика. Диаграмма, подобная линии регрессии на графике, необязательна, но она обеспечивает визуальное представление расчета, облегчая его понимание. В других случаях используется формула y = Y - ȳ обозначает общую сумму квадратов.
Регрессионная сумма квадратов
Сумма квадратов регрессии показывает, насколько хорошо регрессионная модель отражает моделируемые данные. Сумма квадратов усложняется, когда специалисты используют ее для расчета суммы квадратов в регрессионном анализе. Из-за этих сложностей специалисты очень редко выполняют этот расчет вручную. Вместо этого они используют программы для расчета результатов.
При вычислении суммы квадратов регрессии более высокая сумма квадратов регрессии указывает на то, что модель не очень хорошо подходит к данным. Меньшая сумма квадратов регрессии указывает на то, что модель хорошо подходит к данным.
Остаточная сумма квадратов
Остаточная сумма квадратов показывает, какую часть вариации зависимой переменной ваша модель не объясняет. Она измеряет вариацию ошибок в регрессионной модели, то есть показывает величину вариации зависимой переменной. Это сумма квадратов разницы между фактическим значением Y и предсказанным значением Y.
При расчете остаточной суммы квадратов более низкая остаточная сумма квадратов показывает, что регрессионная модель лучше объясняет данные. Более высокая сумма квадратов регрессии показывает, что регрессионная модель плохо справляется с объяснением данных.
- indeed.com
Поделиться