Регрессионный анализ - это, пожалуй, наиболее широко используемая статистическая техника для исследования или оценки взаимосвязи между зависимыми и набором независимых объясняющих переменных.
Он также используется как общий термин для различных методов анализа данных, которые применяются в качественных исследованиях для моделирования и анализа многочисленных переменных. В методе регрессии зависимая переменная является предиктором или объясняющим элементом, а зависимая переменная - результатом или ответом на определенный запрос.
Content Index
- Регрессионный анализ: Определение
- Типы регрессионного анализа
- Линейный регрессионный анализ
- Логистический регрессионный анализ
- Полиномиальный регрессионный анализ
- Пошаговый регрессионный анализ
- Регрессионный анализ гребня
- Регрессионный анализ Лассо
- Регрессионный анализ эластичной сети
- Использование регрессионного анализа в маркетинговых исследованиях
- Как регрессионный анализ позволяет получить информацию из опросов
- Преимущества использования регрессионного анализа в онлайн-опросе
- Получение доступа к предиктивной аналитике
- Повышение операционной эффективности
- Количественная поддержка принятия решений
- Предотвращение ошибок, возникающих из-за интуиции
Регрессионный анализ: Определение
Анализ регрессии часто используется для моделирования или анализа данных. Большинство аналитиков используют его для понимания взаимосвязи между переменными, которая в дальнейшем может быть использована для прогнозирования точного результата.
Пример - Предположим, компания по производству безалкогольных напитков хочет расширить свое производство на новое место. Прежде чем двигаться дальше, компания хочет проанализировать свою модель получения дохода и различные факторы, которые могут на нее повлиять. Поэтому компания проводит онлайн-опрос с помощью специальной анкеты.
После использования регрессионного анализа компании становится проще проанализировать результаты опроса и понять взаимосвязь между различными переменными, такими как электричество и выручка - здесь выручка является зависимой переменной. Кроме того, понимание взаимосвязи между различными независимыми переменными, такими как цены, количество работников и логистика, и выручкой помогает компании оценить влияние различных факторов на продажи и прибыль компании.
Исследователи часто используют этот метод для изучения и поиска корреляции между различными переменными, представляющими интерес. Он дает возможность оценить влияние различных независимых переменных на зависимую переменную. В целом, регрессионный анализ - это метод, который экономит дополнительные усилия исследователей по организации многочисленных независимых переменных в таблицы и тестированию или расчету их влияния на зависимую переменную. Различные виды аналитических методов широко используются для оценки новых бизнес-идей и принятия обоснованных решений.
Create a Free Account
Типы регрессионного анализа
Исследователи обычно начинают с изучения линейной и логистической регрессии. Из-за широкой известности этих двух методов и простоты их применения многие аналитики думают, что существует только два типа моделей. Каждая модель имеет свою особенность и способность работать при соблюдении определенных условий. В этом блоге рассказывается о широко используемых семи типах методов регрессионного анализа, которые можно применять для интерпретации бесчисленного количества данных в самых разных форматах.
Линейный регрессионный анализ
Это один из наиболее широко известных методов моделирования, поскольку он является одним из первых элитных методов регрессионного анализа, взятых на вооружение людьми в период обучения прогностическому моделированию. Здесь зависимая переменная является непрерывной, а независимая переменная чаще всего непрерывная или дискретная с линейной линией регрессии.
Обратите внимание, что в множественной линейной регрессии имеется более одной независимой переменной, а в простой линейной регрессии - только одна независимая переменная. Таким образом, линейную регрессию лучше использовать только тогда, когда существует линейная связь между независимой и зависимой переменными
Пример: Бизнес может использовать линейную регрессию для измерения эффективности маркетинговых кампаний, ценообразования и рекламных акций для продаж продукта. Предположим, компания, продающая спортивное оборудование, хочет понять, принесли ли средства, которые они вложили в маркетинг и брендинг своей продукции, существенную прибыль или нет. Линейная регрессия - лучший статистический метод для интерпретации результатов. Самое лучшее в линейной регрессии то, что она также помогает проанализировать неясное влияние каждого маркетингового и брендингового мероприятия, контролируя при этом потенциал составляющих для регулирования продаж. Если компания проводит две или более рекламных кампаний одновременно, например, одну на телевидении и две на радио, то линейная регрессия может легко проанализировать как независимое, так и комбинированное влияние совместного проведения этих рекламных кампаний.
Логистический регрессионный анализ
Логистическая регрессия обычно используется для определения вероятности события=успеха и события=неудачи. В тех случаях, когда зависимая переменная является бинарной, например, 0/1, истина/ложь, да/нет, используется логистическая регрессия. Таким образом, можно сказать, что логистическая регрессия используется для анализа закрытых вопросов в опросе или вопросов, требующих числового ответа в опросе.
Обратите внимание, что логистическая регрессия не требует линейной зависимости между зависимой и независимой переменными, как линейная регрессия. Логистическая регрессия применяет нелинейное преобразование логарифма для прогнозирования отношения шансов, поэтому она легко справляется с различными типами отношений между зависимой и независимой переменными.
Пример: Логистическая регрессия широко используется для анализа категориальных данных, особенно для данных с двоичными ответами, при моделировании бизнес-данных. Чаще всего логистическая регрессия используется, когда зависимая переменная является категориальной, например, чтобы предсказать, является ли заявление о здоровье, сделанное человеком, реальным(1) или мошенническим, чтобы понять, является ли опухоль злокачественной(1) или нет. Предприятия используют логистическую регрессию, чтобы предсказать, купят ли потребители в определенной демографической группе их продукт или купят у конкурентов на основе возраста, дохода, пола, расы, штата проживания, предыдущей покупки и т.д.
Полиномиальный регрессионный анализ
Полиномиальная регрессия обычно используется для анализа криволинейных данных, что происходит, когда мощность независимой переменной больше 1. В этом методе регрессионного анализа линия наилучшего соответствия никогда не является "прямой линией", а всегда представляет собой "кривую линию", подходящую к точкам данных.
Обратите внимание, что полиномиальную регрессию лучше использовать, когда некоторые переменные имеют экспоненты, а некоторые не имеют их. Кроме того, она может моделировать нелинейно разделимые данные, предоставляя свободу выбора точной экспоненты для каждой переменной, а также полный контроль над доступными функциями моделирования.
Пример: Полиномиальная регрессия в сочетании с анализом поверхности отклика считается сложным статистическим подходом, обычно используемым в исследованиях обратной связи с несколькими источниками. Полиномиальная регрессия используется в основном в отраслях, связанных с финансами и страхованием, где связь между зависимой и независимой переменной криволинейна. Предположим, человек хочет составить бюджет планирования расходов, определив, сколько времени потребуется, чтобы заработать определенную сумму денег. Полиномиальная регрессия, принимая во внимание его/ее доходы и прогнозируя расходы, может легко определить точное время, которое ему/ей нужно работать, чтобы заработать конкретную сумму.
Пошаговый регрессионный анализ
Это полуавтоматизированный процесс, с помощью которого строится статистическая модель путем добавления или удаления переменных, зависящих от t-статистики их расчетных коэффициентов. При правильном использовании пошаговая регрессия обеспечит вас более мощными данными, чем любой другой метод. Она хорошо работает, когда вы работаете с большим количеством независимых переменных. Он просто отлаживает модель анализа путем случайного перебора переменных. Пошаговый регрессионный анализ рекомендуется использовать при наличии нескольких независимых переменных, когда выбор независимых переменных осуществляется автоматически без вмешательства человека.
Обратите внимание, что при моделировании пошаговой регрессии переменная добавляется или вычитается из набора объясняющих переменных. Набор добавляемых или удаляемых переменных выбирается в зависимости от тестовой статистики оцениваемого коэффициента.
Пример: Предположим, у вас есть набор независимых переменных, таких как возраст, вес, площадь поверхности тела, продолжительность гипертонии, базальный пульс и индекс стресса, на основе которых вы хотите проанализировать их влияние на кровяное давление. В пошаговой регрессии автоматически выбирается наилучшее подмножество независимых переменных. Она либо начинается с выбора ни одной переменной для дальнейшего продвижения (поскольку добавляется по одной переменной за раз), либо начинается со всех переменных в модели и продвигается назад (удаляется по одной переменной за раз). Таким образом, используя регрессионный анализ, можно рассчитать влияние каждой или группы переменных на артериальное давление.
Регрессионный анализ
Регрессия основана на обычном методе наименьших квадратов, который используется для анализа данных с мультиколлинеарностью (данные, в которых независимые переменные сильно коррелируют). Коллинеарность можно объяснить как почти линейную связь между переменными. При наличии мультиколлинеарности оценки по методу наименьших квадратов будут несмещенными, но если разница между ними больше, то она может быть далека от истинного значения. Однако гребневая регрессия устраняет стандартные ошибки, добавляя некоторую степень смещения к оценкам регрессии с целью получения более надежных оценок.
Обратите внимание, допущения, полученные с помощью гребневой регрессии, аналогичны регрессии наименьших квадратов, единственное различие заключается в нормальности. Хотя значение коэффициента в гребневой регрессии сужается, оно никогда не достигает нуля, что свидетельствует о невозможности выбора переменных.
Пример: Предположим, вы без ума от двух гитаристов, выступающих вживую на мероприятии неподалеку от вас, и вы идете посмотреть их выступление с целью выяснить, кто из них лучший гитарист. Но когда начинается выступление, вы замечаете, что оба играют черно-синие ноты одновременно. Можно ли определить лучшего гитариста по наибольшему влиянию на звук среди них, когда они оба играют громко и быстро? Поскольку оба они играют разные ноты, их существенно трудно различить, что является лучшим случаем мультиколлинеарности, которая, в свою очередь, имеет тенденцию к увеличению стандартных ошибок коэффициентов. Гребневая регрессия решает проблему мультиколлинеарности в подобных случаях и включает оценку смещения или уменьшения для получения результатов.
Регрессионный анализ Лассо
Лассо (оператор наименьшей абсолютной усадки и отбора) похож на гребневую регрессию; однако он использует смещение по абсолютной величине вместо квадратичного смещения, используемого в гребневой регрессии. Он был разработан еще в 1989 году как альтернатива традиционной оценке по методу наименьших квадратов с намерением устранить большинство проблем, связанных с чрезмерной подгонкой, когда данные имеют большое количество независимых переменных. Лассо обладает способностью выполнять оба действия - отбор переменных и регуляризацию вместе с мягким порогом. Применяя регрессию Лассо, становится проще определить подмножество предикторов, чтобы минимизировать ошибки предсказания при анализе количественного отклика.
Обратите внимание, что в модели Лассо коэффициенты регрессии, достигающие нулевого значения после усадки, исключаются из модели. Напротив, коэффициенты регрессии, имеющие значение больше нуля, сильно связаны с переменными отклика, при этом объясняющие переменные могут быть количественными, категориальными или и теми, и другими.
Пример: Предположим, автомобильная компания хочет провести анализ среднего расхода топлива автомобилями в США. Для выборки они выбрали 32 модели автомобилей и 10 характеристик конструкции автомобиля - количество цилиндров, рабочий объем, полная мощность, передаточное число задней оси, вес, время прохождения мили, в/с двигатель, трансмиссия, количество передач и количество карбюраторов. Как вы можете видеть, корреляция между переменной отклика mpg (мили на галлон) чрезвычайно сильно коррелирует с некоторыми переменными, такими как вес, водоизмещение, количество цилиндров и лошадиные силы. Эту проблему можно проанализировать с помощью пакета glmnet в R и использования регрессии Лассо для отбора признаков.
Регрессионный анализ с использованием эластичной сети
Это смесь моделей регрессии гребня и Лассо, обученных с помощью норм L1 и L2. Эластичная сеть создает эффект группировки, при котором сильно коррелированные предикторы имеют тенденцию входить/выходить из модели вместе. Рекомендуется использовать модель регрессии эластичной сетки, когда количество предикторов намного превышает количество наблюдений.
Обратите внимание, модель регрессии эластичной сетки появилась как вариант модели регрессии лассо, поскольку секция переменных лассо слишком сильно зависела от данных, что делало ее нестабильной. Используя регрессию эластичной сетки, статистики получили возможность преодолеть недостатки регрессии гребня и регрессии Лассо, чтобы получить лучшее из обеих моделей.
Пример: Группа клинических исследований, имеющая доступ к набору данных микрочипов по лейкемии (LEU), была заинтересована в построении диагностического правила на основе уровня экспрессии представленных образцов генов для предсказания типа лейкемии. Набор данных, которым они располагали, состоял из большого количества генов и нескольких образцов. Кроме того, им был предоставлен определенный набор образцов для использования в качестве обучающих образцов, из которых некоторые были заражены лейкемией первого типа (острый лимфобластный лейкоз), а некоторые - лейкемией второго типа (острый миелоидный лейкоз). На обучающих данных были проведены моделирование и подбор параметров настройки методом десятикратного CV. Затем они сравнили эффективность этих методов, вычислив их среднеквадратичную ошибку предсказания на тестовых данных, чтобы получить необходимые результаты.
Использование в маркетинговых исследованиях
В маркетинговом исследовании основное внимание уделяется трем основным матрицам: удовлетворенности клиентов, лояльности клиентов и пропаганде клиентов. Помните, что хотя эти матрицы говорят нам о состоянии здоровья и намерениях клиентов, они не говорят нам о способах улучшения положения. Поэтому углубленный опрос, направленный на выяснение у потребителей причин их неудовлетворенности, безусловно, является способом получить практическую информацию.
Однако было установлено, что люди часто затрудняются изложить свою мотивацию или демотивацию, описать свою удовлетворенность или неудовлетворенность. Кроме того, люди всегда придают излишнее значение некоторым рациональным факторам, таким как цена, упаковка и т. д. В целом, он выступает в качестве инструмента прогнозирования и анализа в маркетинговых исследованиях.
При использовании в качестве инструмента прогнозирования регрессионный анализ может применяться для определения показателей продаж организации с учетом внешних рыночных данных. Транснациональная компания проводит маркетинговое исследование, чтобы понять влияние различных факторов, таких как ВВП (валовой внутренний продукт), ИПЦ (индекс потребительских цен) и других подобных факторов, на ее модель получения доходов. Очевидно, что регрессионный анализ с учетом прогнозируемых маркетинговых показателей был использован для прогнозирования ориентировочного дохода, который будет получен в будущих кварталах и даже в будущих годах. Однако чем дальше в будущее, тем более ненадежными будут становиться данные, оставляя большую погрешность.
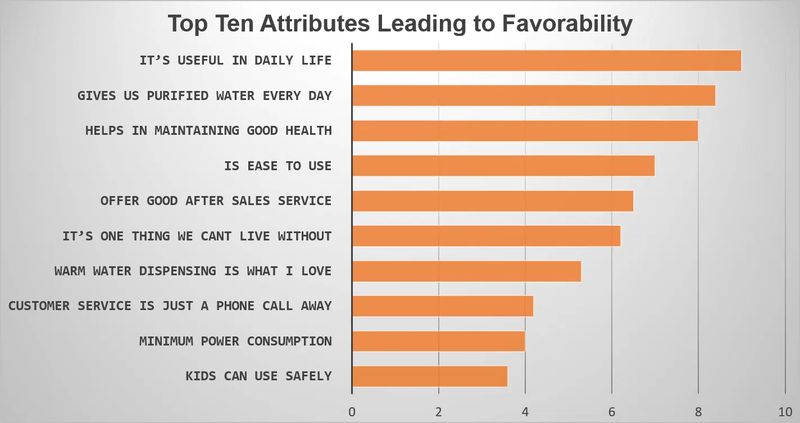
Пример: Компания по производству очистителей воды хотела понять, какие факторы приводят к благосклонности к бренду. Опрос был лучшим средством для установления контакта с существующими и потенциальными клиентами. Был запланирован крупномасштабный опрос потребителей и подготовлен сдержанный вопросник с использованием лучшего инструмента для проведения опроса. В ходе опроса был задан ряд вопросов, касающихся бренда, благоприятности, удовлетворенности и вероятной неудовлетворенности. После получения оптимальных ответов на вопросы анкеты был проведен регрессионный анализ, который позволил выявить десять основных факторов, определяющих благоприятность бренда. Все десять полученных атрибутов (упомянутых на изображении ниже) тем или иным образом подчеркивали свою важность в влиянии на благоприятность конкретного бренда очистителя воды.
Как регрессионный анализ позволяет получить сведения из опросов
Провести регрессионный анализ с помощью Excel или SPSS несложно, но при этом необходимо понимать важность четырех чисел для интерпретации данных.
Первые два числа из четырех напрямую относятся к самой регрессионной модели.
F-значение: Оно помогает измерить статистическую значимость модели исследования. Помните, что F-значение, значительно меньшее 0,05, считается более значимым. F-значение менее 0,05 гарантирует, что результаты анализа опроса не случайны.
- R-квадрат: Это значение, при котором независимая переменная пытается объяснить величину изменения зависимой переменной. Если значение R-Squared равно 0,7, это означает, что 70% движения зависимой переменной может быть объяснено протестированной независимой переменной. Это означает, что результаты анализа опроса, которые мы получим, имеют высокую предсказательную природу и могут считаться точными.
Два других числа относятся к каждой из независимых переменных при интерпретации регрессионного анализа.
- P-Value: Как и F-значение, P-значение имеет большое статистическое значение. Более того, здесь оно показывает, насколько значимым и статистически значимым является влияние независимой переменной. Опять же, мы ищем значение менее 0,05.
- Четвертое число относится к коэффициенту, полученному после измерения влияния переменных. Например, мы тестируем несколько независимых переменных, чтобы получить коэффициент, который говорит нам, "на какую величину, как ожидается, увеличится зависимая переменная, если независимые переменные (которые мы рассматриваем) увеличатся на единицу при неизменном значении всех остальных независимых переменных". В некоторых случаях простой коэффициент заменяется стандартизированным коэффициентом, демонстрирующим вклад каждой независимой переменной в перемещение или изменение зависимой переменной.
Create a Free Account
Преимущества использования регрессионного анализа в онлайн-опросе
Получите доступ к предиктивной аналитике:
Знаете ли вы, что использование регрессионного анализа для понимания результатов бизнес-опроса - это как способность раскрыть будущие возможности и риски?
К примеру, увидев определенный рекламный слот на телевидении, мы можем предсказать точное количество предприятий, используя эти данные для оценки максимальной ставки за этот слот. Финансовая и страховая отрасли в целом во многом зависят от регрессионного анализа данных опросов, позволяющего выявить тенденции и возможности для более точного планирования и принятия решений.
Повышение операционной эффективности:
Знаете ли вы, что предприятия используют регрессионный анализ для оптимизации своих бизнес-процессов?
Например, перед запуском новой линейки продуктов предприятия проводят опрос потребителей с целью лучше понять влияние различных факторов на производство, упаковку, распространение и потребление этого продукта. Предвидение на основе данных помогает устранить из процесса принятия решений догадки, гипотезы и внутреннюю политику. Более глубокое понимание областей, влияющих на операционную эффективность и доходы, приводит к лучшей оптимизации бизнеса.
Количественная поддержка принятия решений:
Сегодня бизнес-опросы генерируют множество данных, связанных с финансами, доходами, операциями, закупками и т.д., и владельцы бизнеса сильно зависят от различных моделей анализа данных для принятия обоснованных бизнес-решений.
Например, регрессионный анализ помогает предприятиям принимать обоснованные стратегические решения в отношении рабочей силы. Проведение и интерпретация результатов опросов сотрудников, таких как опрос вовлеченности сотрудников, опрос удовлетворенности сотрудников, опрос об улучшении работы работодателя, опрос о выходе сотрудников из компании и т. д., помогает лучше понять взаимоотношения между сотрудниками и предприятием. Это также помогает получить объективное представление об определенных проблемах, способных повлиять на культуру труда, рабочую среду и производительность организации. Более того, благодаря разумным интерпретациям, ориентированным на бизнес, он превращает огромную кучу необработанных данных в действенную информацию для принятия более обоснованных решений.
Предотвратить ошибки, возникающие из-за интуиции:
Зная, как использовать регрессионный анализ для интерпретации результатов опроса, можно легко предоставить фактическую поддержку руководству для принятия обоснованных решений. Но знаете ли вы, что он также помогает избежать ошибок в суждениях?
Например, менеджер торгового центра считает, что если он продлит время закрытия торгового центра, то это приведет к увеличению продаж. Регрессионный анализ опровергает это мнение, предсказывая, что увеличение выручки за счет роста продаж будет недостаточным для покрытия возросших операционных расходов, вызванных увеличением продолжительности рабочего дня.
- questionpro
Поделиться